高观点分析学自学指导

第一章 学习指导

本章小结

本章是全书的数学理论的基础。本章的主要内容是：

1．集合：集合的概念，元素与集合的关系，集合的运算，两个集合的笛卡尔积。

2．关系：关系的定义。特别要重视两种特殊的关系，即等价关系与序关系。

等价关系的重要作用是：利用等价关系可以将一个集合划分为若干个两两不交的等价类。

3．映射：设，若任意，存在唯一，使得xFy，则称F是从X到Y的映射。

在中学数学中，强调映射是一个法则，而在本教材中，映射F不是法则。

满射、单射、双射是本章的重要概念。

4．基数：基数是一个很抽象的概念。本章引入基数的概念，它不仅是引入自然数概念的需要，同时也是为了读者加深对等价类的理解。

关键词 集合，交集，并集，差集，关系，等价关系，序关系，映射，单射，满射，双射，运算，基数。

[重、难点解析]

重点：集合，关系，映射，运算，等价关系，序关系。

难点：商集、基数的概念。

（一）关于集合

集合概念是数学中最基本的概念之一，在数学中有其独特的作用。它是现代数学的重要基础，并且应用于许多科学技术领域之中。本节介绍的集合概念和集合运算是本课程的基础，它们在后续各章节中都有应用。因此，我们在学习本节内容时应该理解集合的概念，了解元素与集合、集合与集合之间关系，熟练掌握集合的并、交、差（补）和对称差集的运算，掌握有关运算律的证明方法。

集合是一些具有某种共同特性的、可以区分的若干事物的全体。集合中的事物称为元素或点。

集合有以下三种表示方法：

列举法——列出集合的所有元素，并用花括号括起来。例如。

描述法——将集合中元素的共同属性描述出来。例如。

文氏图——用一个简单的平面区域表示一个集合，用区域内的点表示集合内的元素。如图1-7所示。

1．理解集合概念时应该注意：

（1）集合中的元素是确定的。也就是说，对集合A，任一元素a或者属于A或者不属于A，两者必居其一。若元素a属于集合A，则用表示，若不属于A，则用表示。

（2）集合中的每个元素是可以互相区分的。也就是说，在一个集合中不会重复出现相同的元素。例如集合与是一样的。

（3）组成一个集合的每个元素在该集合中是无次序的，可以任意列出。例如，，是同一集合的三种列举法。

（4）集合的元素可以是任何事物，甚至某一集合可以作为另一集合的元素，例如集合，其中是一个集合，但它又是A的元素。

（5）对于集合元素的个数不作任何限制，它可以是有限个，例如，也可以是无限个，例如。一个集合若由有限个元素组成，称为有限集合；若由无限个元素组成，称为无限集合。

特别地，元素个数为零的集合称为空集，记作。由集合A的所有子集组成的集合，称为A的幂集，记作2^A（或P（A））。若集合A是由n个元素所组成的有限集合，则幂集是由2ⁿ元素组成。

2．了解元素与集合、集合与集合之间关系时应该注意：

元素与集合之间是一种从属或不从属关系，当a 是集合A中的元素，则称a属于A，记作;a不是集合A中的元素，则称a不属于A，记作。

集合与集合之间是一种包含或不包含关系，当两个集保A和B存在关系A包含B或B被A包含，也就是说成立，则称B为A的子集；当，且时，称B为A的真子集。若B不是A的子集，即不成立时，则称A不包含B。

因此，元素与集合、集合与集合之间的关系以及表示这两种关系的符号一定不要混淆。

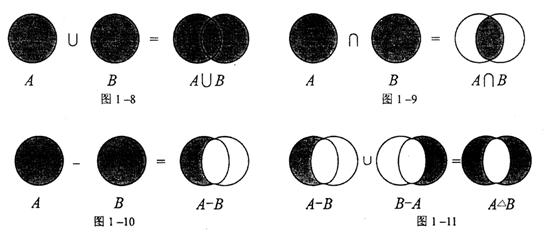
3．通过文氏图进一步理解集合的并、交、差和对称差集的运算，通过练习熟练掌握这些运算。

设A和B是两个任意集合，所有属于A或属于B的元素组成的集合，称为集合A与B的并集，即。

既属于A又属于B的所有元素组成的集合，称为集合A与B的交集，即。

属于A而不属于B的所有元素组成的集合，称为A与B的差（补）集，即。

属于A而不属于B或属于B而不属于A的所有元素组成的集合，称为集合A和B的对称差，即。

如果两个集合A和B没有公共元素，即，称为集合A与B不相交。

并、交、差（补）、对称差集的文氏图如图1-8至图1-11所示：