二、稳定性

     结构稳定性是指结构构件抵抗弯曲变形和失稳破坏的能力，和构件的截面形状，截面积，锚固方式，长度有关，其中长度对构件稳定性的影响最大。

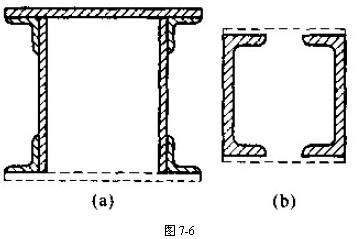
     在轴向拉伸（压缩）杆件的强度计算中，只需其横截面上的正应力不超过材料的许用应力，就从强度上保证杆件的正常工作。但在实际构件中，受压杆件的横截面尺寸一般都较按强度条件算出来的为大，且其横截面的形状往往与梁的横截面形状相仿。例如，钢桁架桥上弦杆（压杆）的横截面（图7-6a）、厂房钢柱的横截面（图7-6b）等。其原因可由一个简单的实验来说明。

     若将钢尺竖立在桌面上，用手压其上端，则当压力不到40N时，钢尺就明显被压弯。显然，这个压力较3.92kN小两个数量级。当钢尺被明显压弯时，就不可能再承受更大的压力。由此可见钢尺的承载能力并不取决于轴向压缩的压缩强度，而是与钢尺受压是变弯有关。维持需要提高压杆的弯曲刚度。同理将一张平的卡片纸放在桌上，其自重就可能使其变弯。若把卡片纸折成类似角钢的形状，就须在其顶端放一个轻砝码，才能使其变弯。若将纸片卷成圆筒形，则虽放上一个轻砝码，也不能使其变弯。这表明压杆是否变弯，与杆横截面的弯曲刚度有关。而起实际压杆在制造时其轴线不可避免会出现初曲率，作用在压杆上外力的合力作用线也不可能毫无偏差地与杆的轴线重合，压杆的材料本身也不可避免的存在不均匀性。这些因素都可能是压杆在外力作用下除发生轴向压缩变形外，还发生附加的弯曲变形。

     为了便于说明这个问题，可将这些因素用外压力的偏心来模拟。压杆在偏心压力作用下，即使偏心矩很小，压杆的次要变形--弯曲变形也有可能随着压力的增大而迅速增长，并逐渐转化为主要变形，从而导致压杆丧失承载能力。

     如上所述，实际压杆受压力作用时，将会发生不同程度的压弯现象，但在对压杆的承载能力进行理论研究时，通常将压杆抽象为由均质材料制成、轴线为直线，且外力作用线与压杆重合的理想"中心受压直杆"的力学模型。在这一力学模型中，由于不存在使压杆变弯的初始因素，因此在轴向压力下就不可能发生弯曲现象。

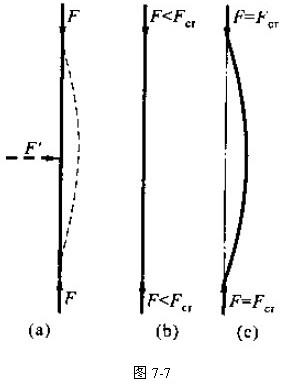
     为此在分析中心受压直杆时，当压杆承受轴向压力（图7-7a中的力F）后，假象的在杆上施加一微小的横向力（图7-7a中的力F'）使杆发生弯曲变形，然后撤去横向力，试验表明，当轴向力不大时，撤去横向力后，杆的轴向将恢复其原来的直线平衡状态（图7-7b），则压杆在直线状态下是稳定的平衡；当轴向力增大到一定的界限时，撤去横向轴力后，杆的轴线将保持弯曲的平衡状态，而不再恢复其原有的直线平衡状态（图7-7c），则压杆原来在直线形态下的平衡是不稳定的平衡。中心受压的直杆在直线形态下的平衡，由稳定平衡转化为不稳定平衡时所受轴向压力的界限值，称为临界压力，或简称临界力，并用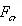表示，中心受压直杆在临界力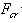作用下，其直线形态的平衡开始丧失稳定，简称为失稳。

     必须指出，通常所说压杆的问定性及其临界压力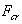下的失稳，是就中心受压直杆的力学模型而言的。对于实际的压杆由于存在述几种导致压杆受压时的弯曲因素，通常可用偏心受压直杆作为其力学模型。实际压杆的平衡稳定问题是在偏心压力作用下，杆的弯曲变形会出现急剧增大而丧失正常的承载能力。