例 2 把 45 换算成二进数。

    解：根据二进数“满二进一”的特点，可以用 2 连续除 45 。

    45 ÷ 2 ＝ 22 （余 1 ）…把 22 进到第二位，余下的 1 是第一位数字；

    22 ÷ 2=11 （余 0 ）…把 11 进到第三位，余下的 0 是第二位数字；

    11 ÷ 2 ＝ 5 （余 1 ）…把 5 进到第四位，余下的 1 是第三位数字；

    5 ÷ 2 ＝ 2 （余 1 ）…把 2 进到第五位，余下的 1 是第四位数字；

    2 ÷ 2 ＝ 1 （余 0 ）…

    1 ÷ 2 ＝ 0 （余 1 ）…

    除到此，就可以写出所求的二进数为：

    45 ＝ 1011012

    为了书写简便，可以用竖式计算：

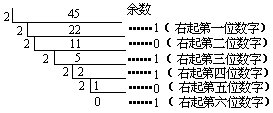
    这种方法通常叫做“二除取余法”。

    3 、其他数制转换的一般方法为：

    （ 1 ）把 r 进制数转换成十进制数，只要把 r 进制数写成 r 的各次幂的和的形式，然后按十进制计算结果。这里 r 是大于 1 的自然数。

    例 1 把八进制数转换成十进数。

    （ 130 ） 8 ＝ 1 × 82 ＋ 3 × 81 ＋ 0 × 80

    = （ 64 ＋ 24 ＋ 0 ） 10

    = （ 88 ） 10

    （ 2 ）把十进制数转换成 r 进制数，采用“ r 除取余法”（这里指十进制数是整数）。即用数 r 连续除十进制整数，取它的每次余数。

    例 3 把（ 173 ） 10 化为一个八进制的数。

    解：

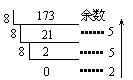
    ∴（ 173 ） 10 ＝（ 255 ） 8

    （三）计算工具：

    计算工具﹝ Calculating Devices ﹞是计算时所用的器具或辅助计算的实物。人们从数学产生之日，便不断寻求能方便进行和加速计算的工具。因此，计算和计算工具是息息相关的。

    中国古代的数学是一种计算数学，当时的人创造了许多独特的计算工具及与工具有关的计算方法。早在公元前 5 世纪 , 中国人已开始用算筹作为计算工具，并在公元前 3 世纪得到普遍的采用，一直沿用了二千年。后来，人们发明了 算盘 ，并在 15 世纪得到普遍采用，取代了算筹。它是在算筹基础上发明的，不但比算筹更加方便实用，把算法口诀化，从而加快了计算速度，还对人类有较强的数学教育功能，因此源用至今，并流传到海外，成为一种国际性的计算工具。

    近代的科学发展促进了计算工具的发展 , 在 1671 年，发明了一种能作四则运算的手摇计算器，是长 1 米 的大盒子。此后，电子 计算器 发展越来越快。现在， 电子计算机 的功能已不止是一种计算工具，它已渗入了人类的活动领域，并改变着整个社会的面貌，使人类社会迈入一个新的阶段。

    老师可以指导学生利用实物计算器或者 Windows 自带的计算器练习计算。还可以利用下面的网上计算器进行训练。

地址一： http://www.aoshu.cn/ceshi/jsp/jisuanqi.asp

           地址二： http://www.hao123.com/haoserver/jishuqii.htm

           附： 《用计算器进行数的简单运算》教学设计