|
中学物理与数学密切联系的教学示例
示例二 抛体运动的几何解法
如果一运动物体所受合力为恒力,且合力方向与物体初速度方向成一定夹角(除
 之外),则物体运动轨迹是抛物线,这是运动称为抛体运动,通常用正交分解法(代数法)处理。利用运动方程(重力场中,忽略空气阻力) 之外),则物体运动轨迹是抛物线,这是运动称为抛体运动,通常用正交分解法(代数法)处理。利用运动方程(重力场中,忽略空气阻力)
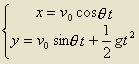
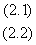
可求出表示体运动的特征及进行有关运算。
运动轨道
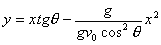 (2.3)
(2.3)
飞行时间
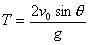 (2.4)
(2.4)
射程
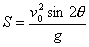 (2.5)
(2.5)
射高
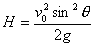 (2.6)
(2.6)
这种解法优点在于与代数知识结合较亲密。缺点是物理意义不明显,解题的数学运算较繁琐。而用几何法处理主要利用矢量合成的三角形法则,整个解题过程主要是解一个或几个三角形,多数情况下,求解过程简单,物理意义明确,能更好地培养利用数学解决物理问题的能力。现结合重力场中,抛体运动主要问题叙述如下:
a)运动性质
抛体运动是 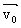 方向的匀速直线运动和 方向的匀速直线运动和
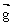 方向的初速度为零的匀变速直线运动的合运动。根据矢量合成的三角形法则其位移和速度的矢量方程为 方向的初速度为零的匀变速直线运动的合运动。根据矢量合成的三角形法则其位移和速度的矢量方程为
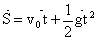 (2.7)
(2.7)
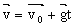 (2.8)
(2.8)
对应的矢量合成图如图 2-1 及图 2-2
所示
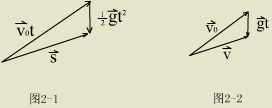
b)运动轨迹
设物体运动的初速度为 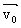 ,加速度为 ,加速度为
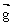 ,物体的初始位置为
O,在 ,物体的初始位置为
O,在 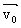 方向取
A , B , C ……诸点,并使 方向取
A , B , C ……诸点,并使 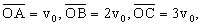 ……,过
A , B , C ……在 ……,过
A , B , C ……在 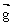 方向取点 方向取点
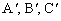 ……,并使 ……,并使
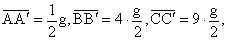 ……,连接
O, ……,连接
O,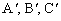 ……诸点的光滑曲线(图
2-3 ),即为质点运动轨迹。 ……诸点的光滑曲线(图
2-3 ),即为质点运动轨迹。
由于 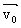 , ,
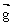 均为常量,因此用几何法决定质点在
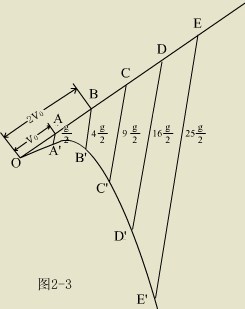
1 , 2 , 3 ,……秒末的位置 均为常量,因此用几何法决定质点在
1 , 2 , 3 ,……秒末的位置 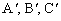 ……
便十分简单。比先用代数法求出系数方程,再用描点法作轨迹图为方便,物理意义更清楚、直观。 ……
便十分简单。比先用代数法求出系数方程,再用描点法作轨迹图为方便,物理意义更清楚、直观。
c)射程、射高、飞行时间
地球表面附近、抛射角为 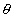 的物体,忽视空气阻力时,运动轨迹为抛物线如图
2-4 ,我们定义 的物体,忽视空气阻力时,运动轨迹为抛物线如图
2-4 ,我们定义
射程 S ——从地面的抛出点到落地点间的水平距离;
飞行时间 T ——从抛出点到落地点所用总时间
射高 H ——地面到轨迹最高点的距离
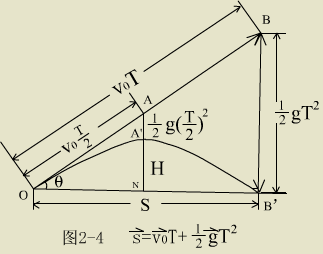
由图 2-4 ,在直角三角形 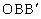 中 中
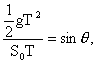 则 则
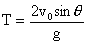
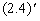
而 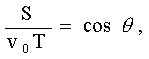 则 则
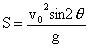
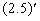
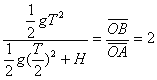 ,则 ,则
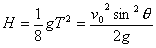
d)计算举例
例1. 在倾角为
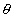 的斜坡上的
O 点沿与水平成倾角 的斜坡上的
O 点沿与水平成倾角 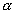 方向向坡顶抛出一石块,石块落在坡上
A 点,如图 2-5 ,已知 方向向坡顶抛出一石块,石块落在坡上
A 点,如图 2-5 ,已知 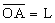 。 。
求:石块抛出的初速度及上述方程所经历的时间。
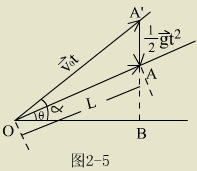
解:据 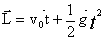 ,对应的矢量合成图的图
2-5 所示 , 在 ,对应的矢量合成图的图
2-5 所示 , 在 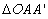 中
, 据正弦定理: 中
, 据正弦定理:
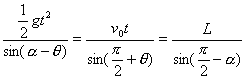
由上式解法:
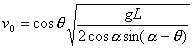
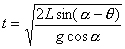
建议大家再用代数法求解该题,并对两种解法加一比较。
例2,一物体以初速度 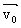 沿水平向上或 沿水平向上或
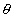 角抛出,问经过多长时间,物体的速度与初速度垂直?此时速度大小是多少?此时物体到抛出点的举距离多大? 角抛出,问经过多长时间,物体的速度与初速度垂直?此时速度大小是多少?此时物体到抛出点的举距离多大?
(设 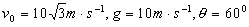 ) )
解:据 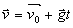
对应的矢量合成图为图2-6( a )
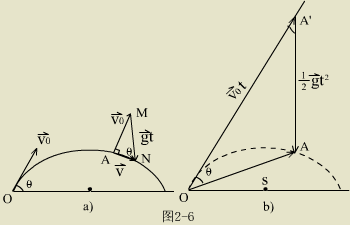
由 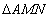 可看出: 可看出:
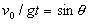
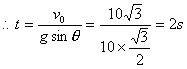
而 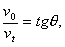
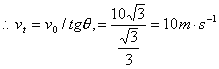
又 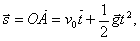 对应的矢量合成图 为图2-6(
b ) 对应的矢量合成图 为图2-6(
b )
在 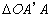 中,据余弦定理, 中,据余弦定理,
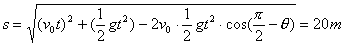
请用代数法求解此题,并与几何体比较。
练习题
斜向上抛出一球,抛出时初速度与水平向上成
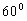 角,1秒后仍上升,但飞行方向已与水平成 角,1秒后仍上升,但飞行方向已与水平成
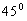 角,求 角,求
1)球上升到最高点所用的时间。
2)球在最高点是的速度。
(2.37 s, 13.4m )
|