|
中学物理与数学密切联系的教学示例
示例 三. 中学物理和数学教学关系
物理和数学是两门关系极为密切的学科。在物理系中经常用数学来表达、推导和计算;而在数学中也广泛应用物理模型。因此,在中学阶段,认真研究物理教学中为何应用数学概念和在数学教学中为何正确应用物理模型。使这两个重要学科彼此促进而不互相牵制,对于学生科学素质的发展与能力的提高具有重要作用。
一、中学物理中经常用到的数学概念和方法
在物理学中,除了大量用到六种运算和布列方程、恒等变换、矢量运算等数学知识外,下到几个方面是较常用到的数学概念和方法。
1.比例的应用
初中二年级物理就接触到比例的概念。为在匀速直线运动中,路程
s 正比于运动的时间 t ;液体内部的压强 P 正比于该位置在液面下的深度 h 。随着学习的深入,又应用到反比。按比例分配、分比、合比等概念。应用这些概念时,务必严格根据物理意义进行教学和学习。例如:
1)一段均匀电阻丝,原来电阻为
R。,把它三等分后拧成一起,求其电阻 R' 设电阻丝原长为 l。横截面积为 S。,电阻率为 ρ ,则根据电阻定律,有
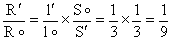
∴ 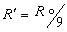
2)已知月球质量是地球质量的
1/81 ,半径约为地球的1/4 ,体重为 60 千克 的宇航员,登上月球后,他的体重将变为多大?
根据万有引律定律,有
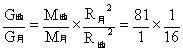 , ,
∴ 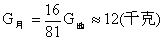
3)根据电容的概念,有
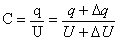
应用分比定理,可得 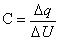 这个重要的关系。 这个重要的关系。
4)对于串联电路,由实验得到
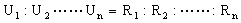
含有电源的均匀电路也是串联电路,上式同样成立,且
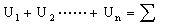
因此,应用分配比例的概念,有
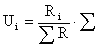
5)成正比的量,可用上法求得,但为成反比,计算就较难。例为,在并联电路中,各支路的电流反比于该支路的电阻,可写为
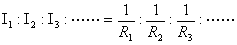
即多支路的电流跟该支路的电阻倒数成正比。由于正确地应用了物理概念和数学知识,在计算时就可收到避难就易的效果。
6)对一个平行板电容器充电,使其电量为
Q 。切断电源并把两板间距离缩小,板间的电场强度将如何变化?
对于带电平行板间电容器,有
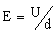 和 和 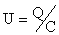
∴ 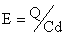
但 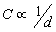 , 即 Cd 乘积不变 , 即 Cd 乘积不变
从而得出结论:板间场强不变
2.不等式的应用
对物理量经常要求指出其上限或下限,有时要指出它可能存在的区别,这就往往用到不等式的概念。
例:一个重为 G 的物体放在倾角为 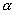 的粗糙斜面上,它们间的静摩擦因数为 的粗糙斜面上,它们间的静摩擦因数为
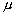 。要使物体静止在斜面上,求施在物体上的,沿斜面向上的拉力
F 的范围,如图 3-1 。要使物体静止在斜面上,求施在物体上的,沿斜面向上的拉力
F 的范围,如图 3-1
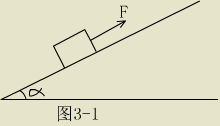
分析:当拉力 F 加大到使物体将要沿斜面向上运动,但又未运动时,有
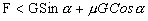 (
3.1 ) (
3.1 )
当拉力 F 小到使物体有 F 滑趋势时,
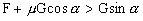
解以上不等式组(3.1),(3.2),得
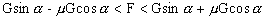
3.极值的应用
物理量间的关系往往以二次函数的形式表示,这就有可能存在极值的问题.
例:一定质量的理想气体,由状态 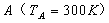 沿直线AB变化到状态B,如图3-2 沿直线AB变化到状态B,如图3-2
所示,求在此状态变化过程中气体的最高温度.
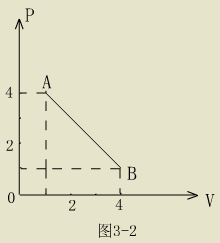
分析:题设的物理过程,由于定量的理想气体,则有
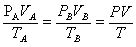
可见,只有当PV的乘积最大时,才会出现T的最大值.图中,P和V的变化关系是线性的
即P+V=5,只有当P=V=2.5时,PV的乘积最大.由于
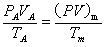
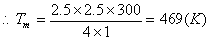
4. 直角坐标图象的应用
物理量之间的函数关系,可用图象表示,为运动学中的
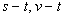 图象,气体中的 图象,气体中的
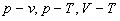 图象等。在运动部分的教学中必须深入阐述图象所表示的物理定义,加深物理与数学相密切联系的理解。 图象等。在运动部分的教学中必须深入阐述图象所表示的物理定义,加深物理与数学相密切联系的理解。
通过图象研究,建立热力学温标,更是用数学方法研究并发展物理学的典型事例
根据 盖 吕萨克
定律和查理定律,有 吕萨克
定律和查理定律,有
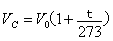 和 和 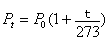
这里, 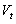 和
t 以及 和
t 以及 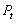 和
t 都不成正比,但这两条直线都跟横坐标有共同交点( -273 , 0 ) 和
t 都不成正比,但这两条直线都跟横坐标有共同交点( -273 , 0 )
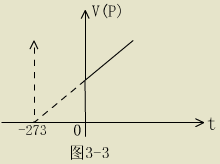
引入热力学温标后,上述方程变为
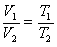 和 和 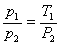
这就极大地简化了计算。当然中必须指出,绝对温度是低温度的极限 .
5 .三角知识的应用,为:
1 ) 三个共点力平衡时,正弦定理的应用;
2 ) 共点力矢量合成的余弦定理;
3 ) 解直角三角形罚用于矢量的正交分解;
4 ) 余弦函数 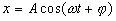 应用于振动,波动及交流电的表示等。 应用于振动,波动及交流电的表示等。
二、应用数学概念时应注意的一些问题
1 .受约于物理现象的本质,数字概念的应用有其局限性。例如:
1 ) R=U/I
,由于电阻 R 一般是常数,因此不能理解为电阻跟电压成正比。只能是电流 I 正比于电压。考虑到电阻的标称功率,电流或电压的值有个上限。
2 )前面提到的电容 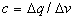 中,由于电容器的带电量不得是它的电压超过电容的耐压值,所以电压的增加是有界的。 中,由于电容器的带电量不得是它的电压超过电容的耐压值,所以电压的增加是有界的。
3 )定量气体在等温变化时
PV= 常量,从数学上看,双曲线应有两支;但从物理本质上,压强和体积不能取负值,因此,它的图象就只能限于第一象限。
2 .物理学中应用数学概念时,又有它的特殊性。例如:
1 )常量建立坐标的方法来处理矢量问题。坐标轴的正方向在物理中原则上是可以任意选取的。这就大大有别于数学中二维空间的正方向的严格规定。各坐标轴的单位长度可以不同,这也是物理的一个特点。
2 )物理中的运算主要有两个特点:
其一带单位运算,或最后用量纲表示的方法,数学中并不采用。
第二,物理研究的是量不是数,因此最后的计算结果一般应一近似值表示。为不能写成
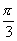 ,而应写成
1.05m 等等。 ,而应写成
1.05m 等等。
3 )方程个数不足的解。在数学中,有几个未知数,就必须有几个方程,否则不能求解;但在物理中,在特定的条件下,方程不足,也可求解。
例:在图 3-4 中,以知电源的电动势
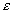 和电阻
R 。的值,当电键 K 接 R 。时电流为 I 1 , 接 R 2 时电流为 I 2 ,求电阻 R X 的值。 和电阻
R 。的值,当电键 K 接 R 。时电流为 I 1 , 接 R 2 时电流为 I 2 ,求电阻 R X 的值。
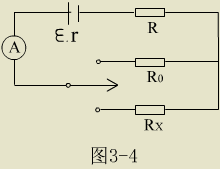
分析:由题设只能列出两个方程,但未知数却有三个:
R , R X ,及内阻 r 。但分析一下电路,发现在任何情况下, R 总是跟内阻串联在一起,因此,可视(
R+r )为一个电阻 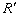 ,则有 ,则有
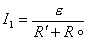 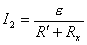
由以上可求 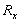 。 。
3. 必须根据物理概念,而不是单纯应用去解物理习题。
例:速度
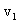 = 2 米 /秒,质量
= 2 米 /秒,质量 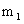 = 3 千克 的物体,与另一静止的质量为
= 3 千克 的物体,与另一静止的质量为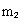 = 2 千克 的物体碰撞。碰撞后两物体的总动能是多少?最小是多少?
= 2 千克 的物体碰撞。碰撞后两物体的总动能是多少?最小是多少?
分析:根据物理概念,只有在弹性碰撞的情况下,动能守恒,因此碰撞后最大总动能就是
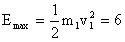 焦耳 焦耳
如果作完全非弹性碰撞初动能损失最大,剩下的最少。此时两物体有共同速度
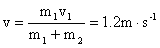 则总动能的最小值是 则总动能的最小值是 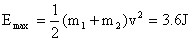
这是完全根据实际物理过程得出的结果。应避免从 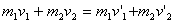 和 和 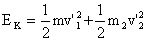 来求 来求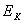 的最大值或最小值,否则,就失去物理学的特点了。 的最大值或最小值,否则,就失去物理学的特点了。
4.应用数学概念和方法时,既应着重从物理现象深入分析它的物理过程,进引如数学处理,空间想象和作图等的能力培养。
三 . 根据学科特点进引教学
中学物理中的主要数学问题如前所述,而中学初高中教学教材中,有关物理的例题和习题也有近 120 个。由此可见物理和数学两门学科间的关系是何等密切。在这两门学科的教学中,应强调既要按本学科的特点,又要考虑对方学科的特点进引教学。物理课绝不应上成数学课;同样,数学课也应保持自己的特色。在物理教学中牵涉到数学问题时,应该使用数学语言,准确的运用数学概念,正确地按数学的要求处理。为在描述正余弦图象时,一样要求最少描 13 个特殊点然后作图。同样,数学教学中遇到物理问题时,也应根据正确的物理概念进引教学。尤其是有些物理问题多次出现更应如此。例如有关运动学问题,随着数学知识的深入,研究方法也相应提高。如初中第一册用一元一次方程研究匀速直线运动;初中第二册用二元一次方程组;初中第三册用二次根式;初中第四册就应用一元二次方程;初中第五册学到直角坐标,用方程距离等概念解题,初中第六册用到一次函数。进入高中后三角函数和参数方程就被用来解决抛体或振动比较复杂的运动了。到高三总复习时,有关高等数学中极限,导数与微分定积分等概念和方法用来处理较复杂的变速直线运动等问题。
|