|
(第三章)第一节 知识及知识的表征
二、知识的表征
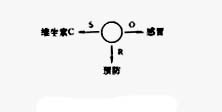
(一)陈述性知识的表征 安德森(1983)认为陈述性知识是以命题和命题网络来表征的。 命题可以用图示加以表示(见图3—2)。在命题的图式中,圆圈或椭圆代表一个命题,S代表主体,O代表客体或对象代表(object),R代表关系(relation)。 图3—2 命题的图式
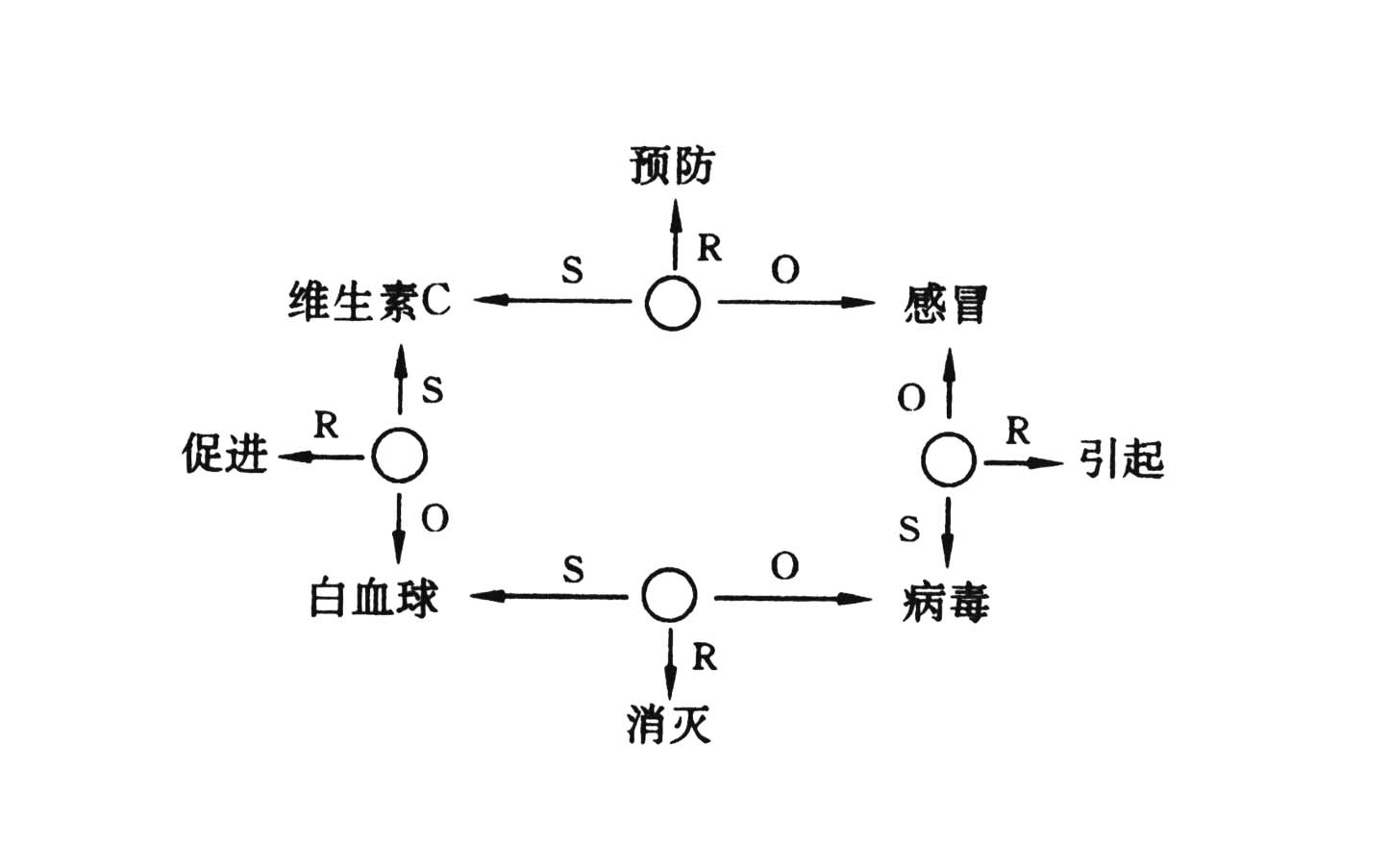
命题网络是由命题之间相互联系而形成的。命题之间由于有相同的论题而相互联系起来,就形成了命题网络。例如“维C预防感冒”、“维C促进白血球的生长”、“白血球消灭病毒”、“病毒引起感冒”四个命题可以形成如下命题网络:
图3—3 命题网络图式 一小段文章是由多个命题而构成的命题网络;一篇文章会构成一个更大的命题网络。因此,一门学科的知识,乃至不同学科的知识通常都是以命题网络的形式贮存于人的长时记忆之中。命题及命题网络被认为是表征陈述性知识的最主要形式。此外,有人(A.Paivio,1971)认为陈述性知识还可以用视觉的或听觉的表象的形式在人的记忆中加以表征,如所见过的各种动物在头脑中形成有关的视觉表象。 (二)程序性知识的表征 产生式这个术语来自数学和计算机科学。认知心理学家纽厄尔和西蒙将这一术语引进心理学。他们认为,人脑和计算机一样都是“物理符号系统”,其功能都是操作符号。计算机由于贮存了一系列以“如果—那么(if-then)”形式编码的规则而具有了完成各种运算和解决问题的智能。同样可以设想,人脑之所以能进行计算和解决问题,也是由于人经过学习,在其头脑中贮存了一系列以“如果—那么”形式表征的规则,这种规则被叫做产生式。 产生式是条件与动作的联结,即在某一条件下会产生某一动作的规则,它由条件项“如果”和动作项“那么”构成。人们在运用程序性知识完成各种活动时,总是根据当前的条件的不同,而采取与之相适应的行动或动作。例如,在分数加法中,如果两个分数的分母相同,那么,我们可以直接将两个分数的分子相加。如果两个分数的分母不同,那么,我们首先必须先通分,找到最小公分母,然后再将分子相加。用产生式可以表示如下(表3—1): 表3—1 分数加法的两个产生式 P1 分母相同的分数加法的产生式 如果 目标是解分数加法 且有两个分数 且两个分数的分母相同 那么 将两个分数的分子相加 P2 分母不同的分数加法的产生式 如果 目标是解分数加法 且有两个分数 且两个分数的分母不同 那么 首先求两个分数的最小公分母
产生式系统是多个产生式的联结。当一个产生式的动作成为另一个产生式的条件时,产生式之间便相互联系起来,构成产生式系统。产生式系统表征了复杂的技能的完成过程。比如,要完成分母不同的分数加法要经过以下九个步骤(周国韬,1997): 1、求最小公分母 2、用最小公分母除以第一个分数的分母 3、将步骤(2)的得数乘以第一个分数的分子 4、将步骤(3)的得数作为分子 5、对第二个分数重复步骤2、3、4 6、将步骤(4)求出的分子相加 7、将步骤(6)的得数作为最后得数的分子 8、将公分母作为最后得数的分母 9、将最后得数中的分子与分母约分后的结果作为最终答案 上述分数加法的前三步的产生式系统如下(表3-2): 表3——2 分母不同的分数加法的前三步的产生式系统 且两个分数的分母不同 那么 首先求两个分数的最小公分母 P2 如果 目标是解分数加法 且有两个分数 且两个分数的分母不同 且两个分数的最小公分母已求出 那么 将求得的最小公分母除以第一个分数的分母 得到结果1 P3 如果 目标是解分数加法 且两个分数的分母不同 且两个分数的最小公分母已求出 且已求出结果1
在上述产生式系统中,第一个产生式的动作成为第二个产生式的条件之一,第二个产生式的动作又成为第三个产生式的条件之一,以此类推,使各个产生式联结成一个复杂的产生式系统,即完成分母不同的分数加法的规则系统。要想获得分数加法的计算技能,学习者首先必须掌握这些规则,然后经过大量的练习形成熟练技能。因此,程序性知识的获得是以陈述性知识的掌握为前提 可见,程序性知识的获得过程就是陈述性知识向技能的转化过程。练习与反馈是陈述性知识转化为程序性知识的重要条件。 |