四 中学物理教学中的数理匹配
　 （一）数理匹配的含义
　　数学与物理是一对形影不离的亲密伙伴。对于物理来说，首先数学是表达物理概念，定律简明而准确的语言，物理学中许多概念的严格定义，是采用数学表达式建立起来的。一个物理过程和定律的描述，往往由若干个物理概念按一定的关系和方式联系起来完成，这一定的关系，就是指各物理概念之间的内在联系，而一定的方式，就是指把个物理量之间的数学关系，用数学等式或不等式表达出来，数学表达式，以至图象，表格等都可以作为物理学的语言，第二。数学为物理学提供了计量和计算工具没有对物理变化情况的定量分析，就谈不上掌握它的变化规律，时只今日，数学的一切成就，几乎全都被物理学家应用上了。数学为物理提供的计量和计算方法也越来越丰富，有效。第三数学是进行抽象思维，逻辑推理的有力工具，数学所使用的一系列逻辑方法，诸如归纳和演绎，分类和比较，分析与综合等等就是在中学的 物理教学中，也的到充分运用。当然，物理学提出的问题也不止一次地推动了教学的发展。因为物理学与教学始终相得益彰，共同发展。这种关系也可借用“匹配”一词概括。物理学中供应能量的一方和使用能量的一方存在一个“匹配”问题，技术上称为能量匹配。加工对象和工具使用也存在一个“匹配”问题，“匹配”就是互相适应，对数学与物理的相互适应，相互配合，我们不妨称为“数里匹配”。
　　（二） 中学物理教学中数理匹配举要
　　“数理匹配”，充分体现在中学物理学的教学之中，举要如下：
[案例16]1．物理函数　 　　　　　　　　　　　　返回
　　函数是中学数学的最基本的概念，一般从初中变量进入数学，学生的数学观念从此开始了质的飞跃，此时学生对物质运动的规律的认识也开始从定性到定量，函数一开始就进入了物理教学。
　　最简单的函数是正比例函数y=kx(k>0)。它正好用于初学物理时，对做匀速直线运动的物体在时刻t所经过的路程s的描述。而且可以通过图象给予形象化的表达，正像数学中用直线表达一次函数一样。当然，物理学决不是抽象的数学，即使是这样简单的函数。也可以让学生通过实验数据引导学生自己总结。
　　中学数理课程中函数主要有以下几种：正比例函数，反比例函数，一次函数，而次函数，有理数函数三角函数，指数函数等。
　　函数的定义域和值域在数学中显得比较抽象，但在中学物理学中，它们的内容却十分具体，丰富，函数（包括公式）都赋予了特定的物理内容，函数的定义域和值域不仅受数学关系的限制。还要受物理量特性和物理规律的约束，稍有疏忽往往引起谬误，即使最简单正比例函数和反比例函数都一样。
[案例17]2．物理学中的平衡原理和方程（方程组）　　返回
　 “平衡”是人们在现实生活中随处可见的一种现象，中学物理学中，有力的平衡，力矩平衡，能量守恒和动量守恒，热平衡等。对一些具体的问题，通过平衡关系列出方程（或方程组）使问题得到解决。力学中的“隔离法”用的就是平衡关系。有时，一个整体“不平衡”的问题，通过“化整为零”，利用平衡关系，使问题 得到解决，比如：一个不平衡的电桥，如图2.4所示，求电流计Ｇ中的电流强度（G的电阻不计）。

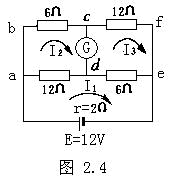
　　这个电路比较复杂，可以把整个电路隔离成一个一个比较简单的回路，然后一个回了一个回路地加以讨论。为此，首先规定好各回路电流的正方向：
　　对EadeE回路，有12I₁+6I₁+2I₁-12I₂-6I₃=12
　　对abcda回路，有8I₂-12I₁=0
　　对cfedc回路，有18I₃-6I₁=0
　　将这三个方程联立解之，即得I₂=4/5,I₃=2/5
　　于是电流计G中的电流是I_g=I₂-I₃=2/5(安培)而方向与I₂的方向相同。
[案例18]3.物理问题的几何化　　　　　　　返回
　　数学中，数与形的结合是一种思想方法这种思想和方法在物理学中得到广泛的应用，一些比较抽象的物理概念和规律的教学，若从数形结合的思想观点出发，恰当地引入物理图象，便可变象为形象、直观。比如，电源输出功率随外电阻变化的规律：

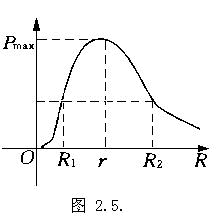
p=ε²R/(R+r)²,如只从该函数关系上讨论，学生必然会感到抽象，难以从整体上把握，不妨定性的划出Ｐ随R变化的函数图像（图2.5），便可从此图像中直观、清晰的看出，随着R的增大,p先增后减，是“单逢”状，并且对同一输出功率p<p_max　，总有两个不同的外电阻R₁,R₂使P(R₁)=P(R₂)=P 。还可以告诉学生，对函数P=ε₂R/(R+r)²,利用简单的高等数学知识便可得到，当R=r时，P为最大．这样将函数关系式与P-R图像结合起来，就能使学生很容易从整体上掌握P随R变化的规律．
　　有些物理问题的求解，简单从数的方面进行分析推导，则相对难度较大、较繁，甚至还求不出结果，但如将问题几何化，应用物理图象进行综合分析，则可事半功倍，建议读者不妨通过下面这一问题作一比较。
　　问题：从地面上以初速度２V₀竖直上抛物体A，相隔时间Δt后，再以初速度V0竖直上抛物体B,要使物体在空中相遇应满足什么条件？
　　对此问题，如只从数值方面去考虑，是比较复杂的，但依据S=V₀t-gt²/2作图象，则问题很容易解决。读者不妨试一试。（答案：2V₀/g<Δt<4V₀/g）

　　中学物理教学中，物理问题的几何化随处可见，包括高中阶段解析几何以及矢量和旋转矢量的应用。但一定要注意，物理过程，物理过程的形象化，几何化，不要脱离具体的物理概念所固有的特征，图形的几何意义应受到物理实际内容的制约。例如：一定质量的理想气体作等温变化时，满足波意耳定律PV=C，从数学图形上看，这是两只关于原点对称的双曲线，但只有位于第一象限中的双曲线才具有实际物理意义。

　　数理匹配，我们的目的始终是物理的。