二、刚体、变形体
     高中物理中我们并未特别说明我们研究的对象为刚体，不过在高中物理中对于我们研究的对象基本都看成是理想的刚体。现在我们来给刚体下个定义，刚体是在外力作用下形状和尺寸都不改变的物体。实际上，任何物体受力的作用后都发生一定的变形，但在一些力学问题中，物体变形这一因素与所研究的问题无关或对其影响甚微，这时可将物体视为刚体，从而使研究的问题得到简化。

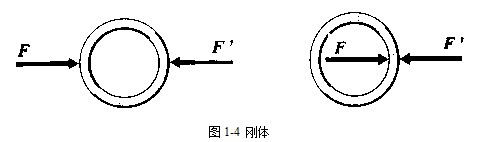
     变形体受荷载作用时将产生变形。当荷载撤去后，可完全消失的变形称为弹性变形；不能恢复的变形称为塑性变形或残余变形。

     三、力矩

     力对点之矩
     力不仅仅可以改变物体的移动状态，而且还能改变物体的转动状态。力使物体绕某点转动的力学效应，称为力对该点之矩。以扳手旋转螺母为例，如图1-6所示，设螺母能绕点O转动。由经验可知，螺母能否旋动，不仅取决于作用在扳手上的力F的大小，而且还与点O到F的作用线的垂直距离d有关。因此，用F与d的乘积作为力F使螺母绕点O转动效应的量度。其中距离d称为F对O点的力臂，点O称为矩心。由于转动有逆时针和顺时针两个转向，则力F对O点之矩定义为：力的大小F与力臂d的乘积冠以适当的正负号，以符号mo(F) 表示，记为

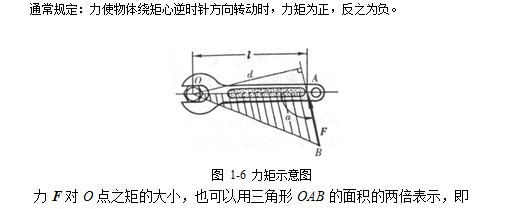
     在国际单位制中，力矩的单位是牛[顿]o米（Noom）或千牛[顿]·米（kNom）。

     由上述分析可得力矩的性质：
     （1）力对点之矩，不仅取决于力的大小，还与矩心的位置有关。力矩随矩心的位置变化而变化。

     （2）力对任一点之矩，不因该力的作用点沿其作用线移动而改变，再次说明力是滑移矢量。

     （3）力的大小等于零或其作用线通过矩心时，力矩等于零。

     在物理学的基础上，现在考察空间任意力对某一点之矩。

     如图1-7所示，设力

O点到力F 作用点A 的矢量称为矢径,

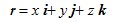
定义：力对O点之矩等于矢径r 与力F 的矢积，即

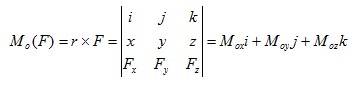
MOx，MOy，MOz 分别称为MO（F）在过O 点的x、y、z 轴上的投影。
根据式（1-3）有

     力对轴之矩