性质Ⅱ 力偶对刚体的作用效应，仅是使刚体转动。力偶矩矢量是力偶使刚体产生转动效应的量度。

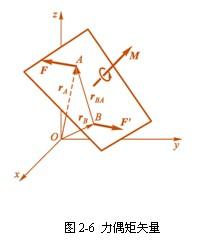
     考察图2-6 所示由F 和F 组成的力偶（F ，F ），其中F =-F 。O点为空间的任意点。力偶（F，F ）对O点之矩定义为

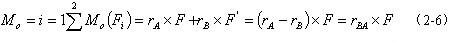
     其中r BA 为自B 至A 的矢径。

     也可以任取其它各点，也可以得到同样结果。这表明：力偶对点之矩与点的位置无关。于是，在不失一般性的前提下，式（2-6）也可以写成

     其中的M 称为力偶矩矢量。

     我们不难看出，力偶矩矢量只有大小和方向，与力矩中心O 点无关，故为自由矢。

     根据力偶对刚体的转动效应，除了用两个力（ F ,F ）和力偶矩矢量M 表示外，还可以用力偶作用面内的旋转箭头表示，如图2-7 所示。

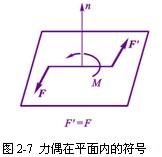
     根据力偶的基本性质，可以得到两个推论：

     推论1 只要保持力偶矩矢量不变，力偶(图2-8a)可在其作用面内任意移动和转动(图2-8b、c)，也可以连同其作用面一起、沿着力偶矩矢量作用线方向平行移动(图2-8d),而不会改变力偶对刚体的运动效应。

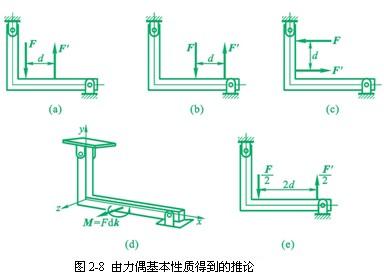
     推论2 只要保持力偶矩矢量不变，可以同时改变组成力偶的力和力偶臂的大小，而不会改变力偶对刚体的作用效应(图2-8e)。

这两条推论可以应用力偶的基本性质加以证明，有兴趣的学员可以尝试证明下。