第三节 力系的简化

     所谓力系的简化，就是将由若干力和力偶所组成的一般力系，变为一个力，或一个力偶，或者一个力和一个力偶的简单的、但是等效的情形。这一过程称为力系的简化。力系简化的基础是力向一点平移定理。

     一、力的平移定理

     作用在刚体上的力如果沿其作用线移动，并不会改变力对刚体的作用效应。但是，如果将作用在刚体上的力从其作用点平行移动到另一点，对刚体的运动效应将会发生改变。能不能使作用在刚体上的力从一点平移至另一点，而使其对刚体的运动效应保持不变呢？

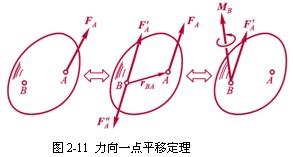
     答案是肯定的。

     图2-11b 中所示之作用在A点的力FA 与作用在B 点的力A F 组成一力偶，其力偶矩矢量为M=rBA× FA，如图2-11c 所示。

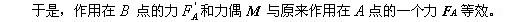
     我们不难发现，这一力偶的力偶矩等于原来作用在A点的力FA 对B 点之矩。

     上述分析结果表明：作用在刚体上的力可以向任意点平移，平移后应为平移后的这一力与一力偶所替代，这一力偶的力偶矩等于平移前的力对平移点之矩。这一结论称为力向一点平移定理。

     力向一点平移的结果: 一个力和一个附加力偶，附加力偶的力偶矩等于原来力对平移点之矩。

     力的平移定理提示了力对刚体产生移动和转动两种运动效应的实质。

     通过打乒乓球的削球、司机开车、用钥匙开门有时钥匙断等情形进一步分析我们可以发现力矩和力偶的区别：力矩和力偶都能使物体转动，但有区别：

     （1）力矩转动须有支点,力偶转动的支点可有可无。

     （2）力矩转动的支点受力,力偶转动的支点不受力