【例3－7】 简单超静定问题。如图3-18(a)所示刚性杆用三根刚度系数均为k的弹簧水平悬吊。今在D处作用铅直方向力F，不计杆重，试求3根弹簧的内力。

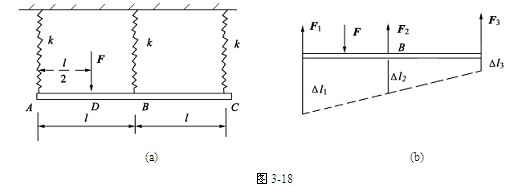
     解 本题所涉及的力系属平面平行力系，有三个未知力，只有两个独立平衡方程，是一次超静定问题尚需建立一个补充方程。设系统受力后，位移如图3-18(b)所示。

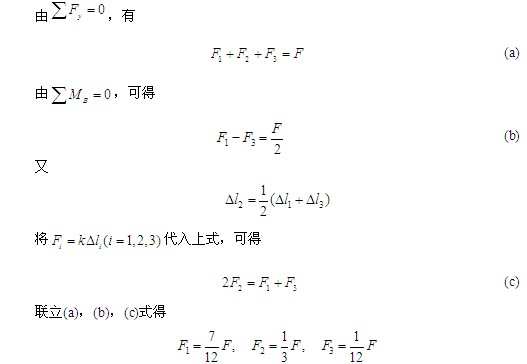
     思考 例3-7图(a)中，若有n根弹簧悬吊，如何求解？

     注意 (1) 求解超静定问题的关键是，由变形情况，通过物理关系，建立包含未知力的补充方程，再与静力平衡方程联立求解。（2）所设未知力的方向与物体变形假设方向要一致。

     二、物体系统平衡问题的解法

     I 一般步骤
     求解物体系统的平衡问题，从整体上说，可分为三个步骤：

     (1) 根据具体问题的已知条件与所求目标，确定先求什么后求什么的整体思路，通常是先分析整体后考虑局部，或先分析局部再研究整体。

     (2) 将所选择的研究对象从所在系统中分离出来，根据分离处的约束性质与已知荷载，正确画出受力图。要注意简化力系的条件。

     (3) 根据受力图提供的力系几何特征，选取适当的投影轴和力矩轴，列出独立的平衡方程求解。为了尽量使平衡方程中只含一个未知量，可选与多个未知力相垂直的轴为投影轴，选与多个未知力相交或平行的轴为力矩轴。