您当前的位置:第三章 >>第三节 物体系统的平衡问题
第三节 物体系统的平衡问题
前面研究了平面力系单个物体的平衡问题,但是在工程结构中往往是由若干个物体通过一定的约束来组成一个系统,这种系统称为物体系统。要应用平衡条件求出平衡系统中各构件的全部未知外力,首先需要判断这些未知外力能否仅用静力平衡方程全部解出。只有在可解的前提下,才能在运用刚体平衡条件范围内进行求解。
一、静定与超静定问题的概念
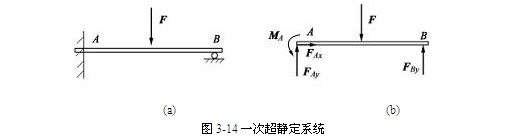
考察一个平衡的物体系统,能否用静力平衡条件求出每个构件的全部外力,从数学意义上说,就是要分析描述平衡系统的独立平衡方程的个数与系统中全部未知量个数。对于几何不变系统,当两者数目相等时可解,这种平衡系统称为静定的;反之,若未知量个数多于独立平衡方程个数,则仅用静力平衡方程不能求出全部未知量,这种系统称为静不定的,又叫超静定的。全部未知量个数与全部独立平衡方程数之差,通常称为系统的超静定次数。如图3-14(a)所示横梁其受力如图3-14(b)所示,为平面一般力系,其中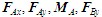 为4个未知约束力,而独立平衡方程只有3个,故该系统为一次超静定系统。
为4个未知约束力,而独立平衡方程只有3个,故该系统为一次超静定系统。
对于由n个承受平面力系的构件所组成的平面几何不变系统,其独立平衡方程个数为3n,全部未知量个数为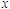 ,则
,则
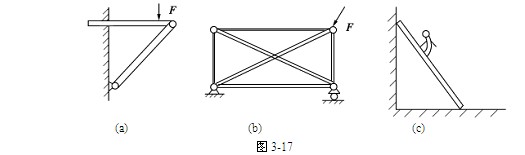
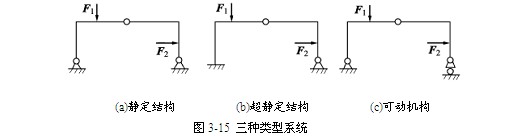
(1) 当 时,为静定系统。如图3-15(a)中
时,为静定系统。如图3-15(a)中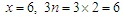 ,它是静定结构。
,它是静定结构。
(2) 当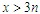 时,为超静定系统。如图3-15(b)中
时,为超静定系统。如图3-15(b)中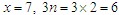 ,它是一次超静定结构。
,它是一次超静定结构。
对于平面机构系统,有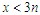 ,系统可动。如图3-15(c)中,
,系统可动。如图3-15(c)中,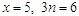 ,它是有一个自由度的机构,这种系统显然不能作为结构使用。
,它是有一个自由度的机构,这种系统显然不能作为结构使用。
本课程主要研究的为静定系统。
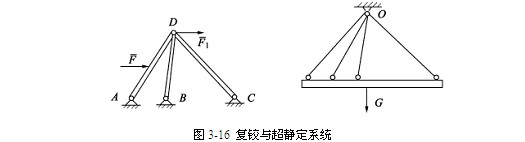
注意 在计算未知量个数时,对于连结两个以上物体的铰(称为复铰),应按拆开时的单铰数计算未知力个数,如图3-16(a)所示;D铰应视为两个单铰,未知量个数为4;在计算独立方程个数时,需先判断力系的类型,如图3-16(b)所示力系属平面汇交力系,只有两个独立平衡方程,为二次超静定系统。
顺便指出,所谓超静定系统,仅仅指由刚体平衡方程不能确定全部未知外力的系统。当把相应物体视为变形体,并引入变形协调方程时,全部外力都能确定。
思考 试判断图中各系统是否静定?