II 典型例题

     (1) 整体“静定”型
     【例3－8】 图3-18(a)所示结构中，C，E处为光滑接触，销钉A，B穿透其连接的各构件，已知尺寸a，b，铅垂力F可以随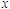的变化而平移。不计自重，求AB杆所受的力。

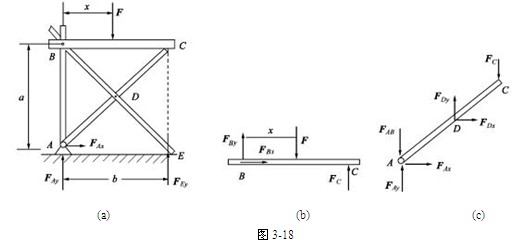
     解 先研究整体，其受力如图(a)所示。

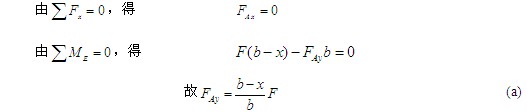
     再研究BC杆，其受力如图(b)所示。由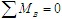，得

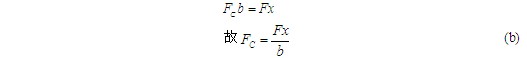
     最后研究AC杆，其受力如图(c)所示，其中 为AB杆对销钉A的作用力(AB是二力杆)。由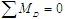，得

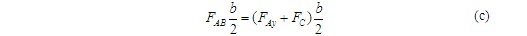
     将式（a）和式（b）代入式（c），得

可见，AB杆受力与x无关。

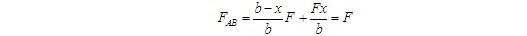
     注意 本题中结构属整体“静定”型，先由整体求出铰A约束力。AB为二力杆，它所受销钉A对它的约束力与其A端对销钉的反作用力等值反向；A处销钉附在AC杆上，使分析过程简化。

     思考 若先研究BC杆，再研究BE杆，如何求出 ？若从研究销钉A平衡入手，如何求出 ？

     (2) 局部“静定”型
     【例3－9】 图(a)所示铰接横梁。已知荷载q，力偶矩M和尺寸a，试求杆的固定端A及可动铰C端约束力。

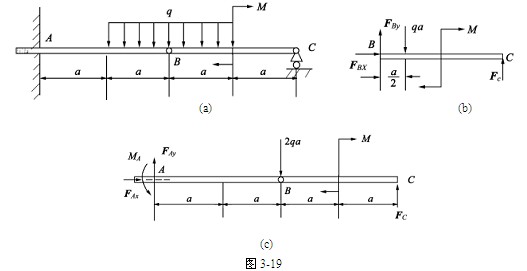
     解 先研究杆BC，其受力如图(b)所示。

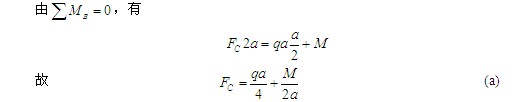
     再研究整体，其受力如图(c)所示。

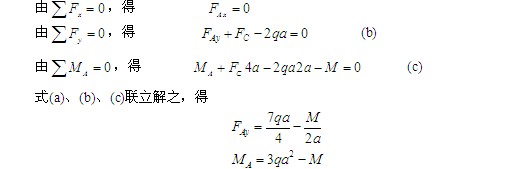
     注意 分析整体“超静定”系统时，可先分析局部“静定”部分，求出相应外力。分布力q的简化，只能在可视为刚体的研究对象上进行，如图(b),(c)所示。

     思考 若在铰B处再加一力 ，如图3-20所示，试问哪些约束力会变化？