(3) 力偶系平衡问题
     【例3－10】 图(a)所示结构中，杆DE的D端为铰，E端光滑搁置，且DE∥AC， ，力偶矩为M，求A，C铰支座约束力。

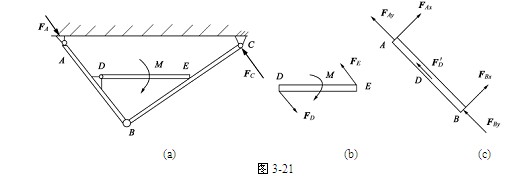
     解 先研究杆DE，其受力如图(b)所示。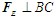，与AB杆平行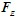， 与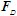组成一力偶。再研究杆AB，其受力如图(c)所示。由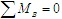得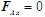。最后研究整体，其受力如图(a)所示。因铰A对AB杆约束力为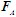，方向沿AB，它与铰C对BC杆约束力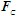组成一力偶。由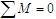，得。

     注意 力偶只能由力偶平衡，由此确定D，C处约束力方向；将杆端力沿杆向正交分解，常使求解简便。

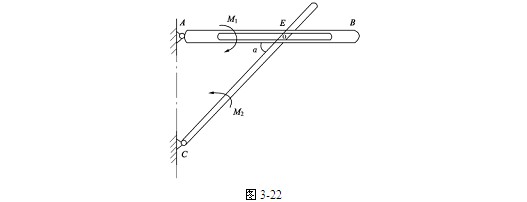
     思考 如图3-22图示光滑导槽机构，CE杆上的销钉E可沿导槽滑动。不计杆重，试分析平衡时两力偶矩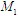和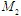大小相等的条件。

     (4) 平面多跨结构
     【例3－11】 图3-23(a)所示平面刚架中，E，F，G为中间铰，A，D为固定铰支座，B，C为可动铰支座，不计自重，在水平力F作用下，求支座A，B，C，D处的约束力。

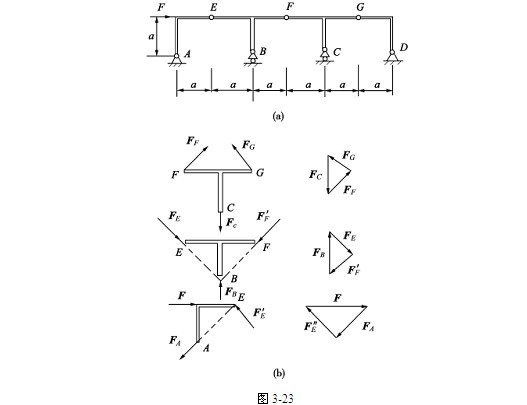
     解 依次研究构件CFG，BEF和AE，其受力如图(b)所示(GD为二力构件)。先由AE半拱的力三角形，得

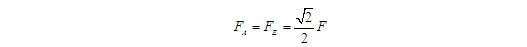
     再由BEF构件的力三角形，得

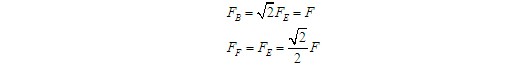
     最后，由CFG构件的力三角形，得

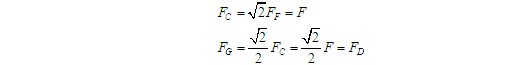
     注意 解此题时需先确定二力构件GD受力方位，其指向可事先假设，再从右向左依次确定各构件所受力的方向。计算时从受已知力的AE构件开始，依次求出各约束力大小。

     由此可见，几何法用于求解三力平衡问题时，一般可归结为解三角形，运算简便；对于三力以上的汇交力系平衡问题，相应的力多边形几何求解复杂，大多采用平衡方程求解。

     思考① 例3-11结构中，若在铰G处增加铅垂向下力 ，结果如何？② 若在EG段受均布荷载q，如何求解？③ 若由图所示三跨结构扩大为n跨后，支座约束力有何规律？