（3）三力矩式
     若二个投影方程全部用力矩方程代替，则有

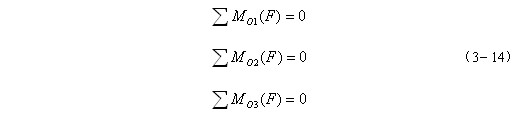
     式中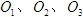，三点不共线。

     同理，由上述三个方程可知，力系不可能简化成为力偶，若简化为合力，则合力要过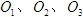三点，但由于此三点不共线，故力系不可能有合力，只能保持平衡。

     需要指出的是：
     （1）上述平衡方程式中所提及的坐标轴和矩心皆可任意选择，但为了避免解联立方程，应使所选坐标轴尽量垂直于未知力，所选矩心位于未知力的交点上（可在研究对象之外）。

     （2）平面任意力系的平衡方程虽然有三种不同的形式，但一个平衡的平面任意力系只能有三个独立的平衡方程，再列出的第四或第五个平衡方程，不再是独立的平衡方程，而是力系平衡必然的结果。在实际应用中，可根据具体情况选择适当形式的平衡方程。为计算方便，应尽量使一个方程中只包含一个未知量。

     三、平面力系的平衡问题求解
     平面任意力系的平衡问题，在工程实际和后续课程中极为常见。平面任意力系的平衡问题包括单个物体和由若干个物体组成的物体系统的平衡问题。我们先讨论单个物体的平衡问题，它是求解物体系统平衡问题的基础，必须熟练掌握，而物体系统的平衡问题将在后面讨论。

     求解单个物体平衡问题的步骤为：

     （1）选取研究对象，取隔离体，画受力图。

     （2）据受力图中力系的特点，灵活地选取投影轴和矩心。投影轴和矩心的选取原则是：使尽可能多的未知力与投影轴垂直，使尽可能多的未知力作用线通过矩心，以求做到列出一个平衡方程，就能求解一个未知量，避免解联立方程组。

     （3）列平衡方程解出所需的未知量。若所得结果为负，则说明负号的含义，而不要改变受力图中原来假设的方向。

     【例3－1】梁AB的A端为固定铰支座，B端为活动铰支座（图3－7a），梁上受集中力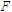与力偶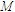的作用。已知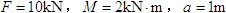求支座A、B处的反力。

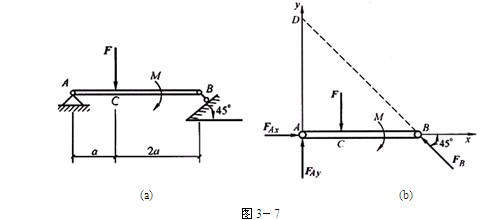
     解 （1）选取研究对象，画受力图。由于已知力和待求力都作用于梁AB上，故选取梁AB为研究对象。梁AB的受力图如图3－7b所示。作用于梁上的主动力有荷载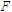、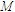，支座反力有和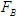，指向假定。这些力组成一个平面任意力系。

     （2）列平衡方程，求约束力。本题有一个力偶，由于力偶在任一轴上投影都为零，故力偶在投影方程中不出现；由于力偶对平面内任一点之矩都等于力偶矩，而与矩心的位置无关，故在力矩方程中可直接将力偶列入。取直角坐标系，如图3－7b所示。

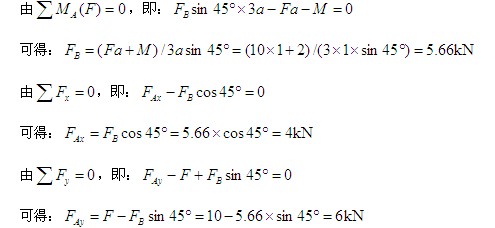
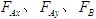均为正值，表示力实际的指向与假定的指向相同（若为负值，则表示力实际的指向与假定的指向相反）。